Skip to contents

Label placement based on a simulation of electrostatic forces

Source: R/aqp-label-placement-solvers.R
electroStatics_1D.Rd

This function attempts to move labels along a 1D coordinate system such that overlap (as specified by threshold) is minimized. An electrostatic simulation applies forces of repulsion between labels that are within thresh (e.g. overlapping) and forces of attraction to a uniformly spaced sequence to iteratively perturb affected labels until either no overlap is reported, or a maximum number of iterations (maxIter) has been reached.

Usage

electroStatics_1D(
  x,
  thresh,
  q = 1,
  chargeDecayRate = 0.01,
  QkA_GrowthRate = 0.05,
  maxIter = 100,
  tiny = 1e-04,
  const = 0.001,
  trace = FALSE,
  ...
)

Arguments

x

numeric vector, pre-sorted sorted, without duplication, describing 1D label (particle) configuration

thresh

numeric, overlap threshold, same as in fixOverlap()

q

numeric, electrical charge (typically between 0.1 and 2)

chargeDecayRate

numeric, exponential decay rate constant for q as a function of iteration i

QkA_GrowthRate

numeric, growth rate constant for Qk applied to attraction to uniform spacing of labels, invoked when rank order is violated during the simulation

maxIter

integer, maximum number of iterations before giving up

tiny

numeric, 0-values replaced by this number to avoid division by 0 and infinite forces

const

numeric, empirical constant added to the 1D electrostatic force equation to dampen oscillation: (Qk * Q1 * Q2) / (d^ex + const)

trace

logical, include diagnostic output

...

not used, absorbs additional arguments to fixOverlap()

Value

When trace = TRUE a list, otherwise numeric vector with converged attribute.

Details

Difficult overlap problems can be addressed by reducing thresh and increasing q. Large values of q can lead to chaotic results.

This function will generate unpredictable output when x contains duplicate values.

This function requires input to be pre-sorted, although interesting "artistic" simulations will often result from unsorted x.

See also

fixOverlap(), SANN_1D()

Author

D.E. Beaudette and K.C. Thompson

Examples


# vector of object locations, with potential overlap
x <- c(1, 2, 3, 3.3, 3.8, 5, 6, 7, 8, 9, 10)

# full diagnostic output
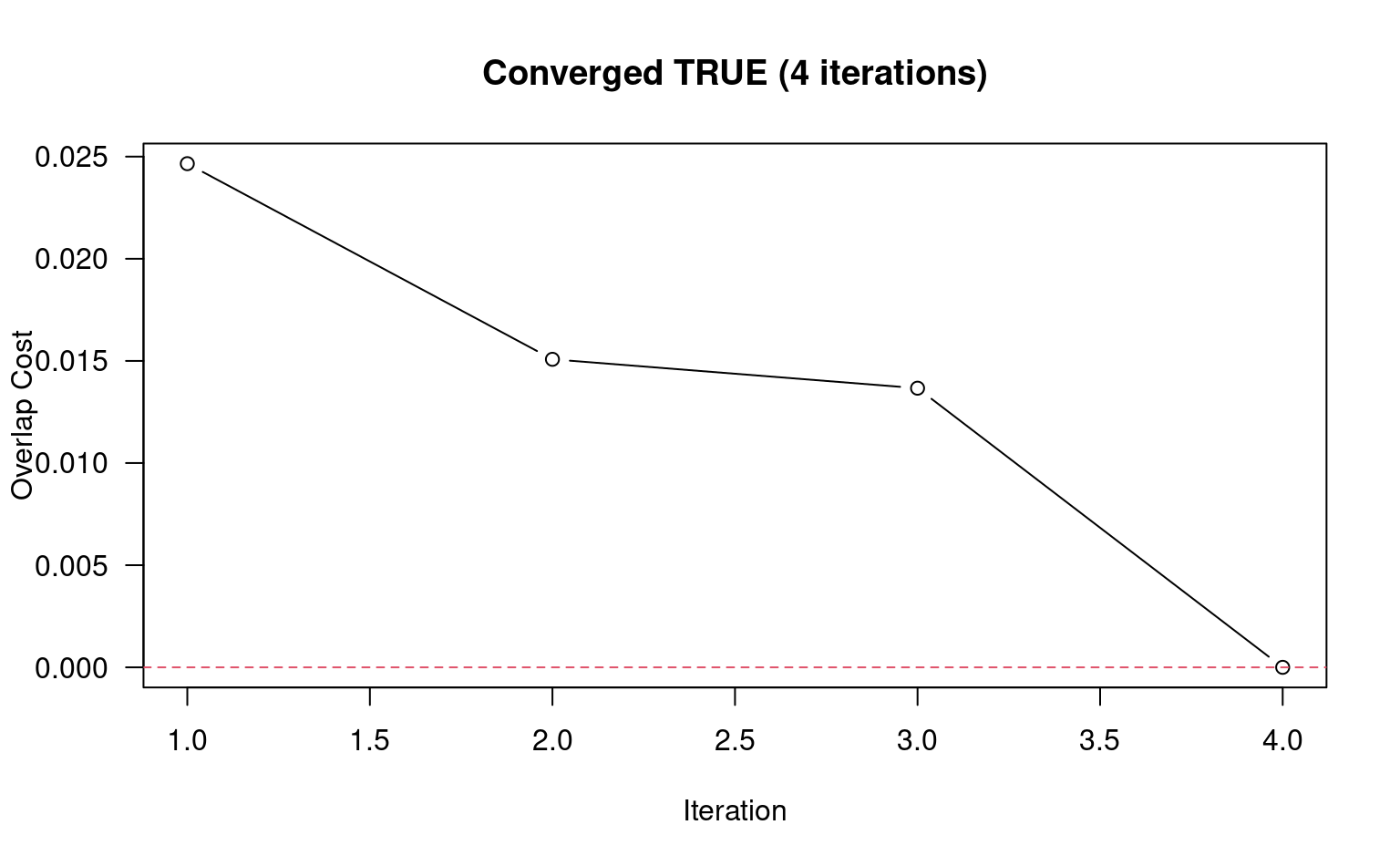
z <- electroStatics_1D(x, thresh = 0.65, trace = TRUE, q = 1)
#> 4 iterations
txt <- sprintf("Converged %s (%s iterations)", z$converged, length(z$cost))

plot(
seq_along(z$cost),
z$cost, 
las = 1, 
xlab = 'Iteration', 
ylab = 'Overlap Cost', 
type = 'b', 
main = txt
)

abline(h = 0, lty = 2, col = 2)


# final configuration only
xnew <- electroStatics_1D(x, thresh = 0.65, q = 1)
#> 4 iterations

# check for convergence
attr(xnew, 'converged')
#> [1] TRUE

# compare original vs. modified
data.frame(orig = x, new = round(xnew, 2))
#>    orig   new
#> 1   1.0  1.00
#> 2   2.0  2.00
#> 3   3.0  2.66
#> 4   3.3  3.35
#> 5   3.8  4.01
#> 6   5.0  5.00
#> 7   6.0  6.00
#> 8   7.0  7.00
#> 9   8.0  8.00
#> 10  9.0  9.00
#> 11 10.0 10.00