Slicing of SoilProfileCollection Objects

slice.fast(object, fm, top.down = TRUE, just.the.data = FALSE, strict = TRUE)

Arguments

object: a SoilProfileCollection
fm: A formula: either integer.vector ~ var1 + var2 + var3 where named variables are sliced according to integer.vector OR where all variables are sliced according to integer.vector: integer.vector ~ ..
top.down: logical, slices are defined from the top-down: 0:10 implies 0-11 depth units.
just.the.data: Logical, return just the sliced data or a new SoilProfileCollection object.
strict: Logical, should the horizonation be strictly checked for self-consistency?

Value

Either a new SoilProfileCollection with data sliced according to fm, or a data.frame.

Details

By default, slices are defined from the top-down: 0:10 implies 0-11 depth units.

References

D.E. Beaudette, P. Roudier, A.T. O'Geen, Algorithms for quantitative pedology: A toolkit for soil scientists, Computers & Geosciences, Volume 52, March 2013, Pages 258-268, 10.1016/j.cageo.2012.10.020.

Author

D.E. Beaudette

Examples


library(aqp)

# simulate some data, IDs are 1:20
d <- lapply(1:20, random_profile)
d <- do.call('rbind', d)

# init SoilProfileCollection object
depths(d) <- id ~ top + bottom
head(horizons(d))
#>   id top bottom name        p1         p2        p3        p4         p5 hzID
#> 1  1   0     28   H1  -8.11480 -4.0385981  2.344391 -4.589098   4.091567    1
#> 2  1  28     33   H2 -12.31050 -5.5446737  7.390140  7.972591   1.350237    2
#> 3  1  33     59   H3 -15.19766 -3.8702909  6.107026  1.339378  -2.038242    3
#> 4 10   0      9   H1  -9.14086 -2.5672940  1.884982  6.057878  -3.203610    4
#> 5 10   9     29   H2 -15.64414 -0.4422915 -3.941346 14.046647 -14.451331    5
#> 6 10  29     59   H3 -20.32191  4.6205974 -5.215878 24.373036 -15.486156    6

# generate single slice at 10 cm
# output is a SoilProfileCollection object
s <- dice(d, fm = 10 ~ name + p1 + p2 + p3)

# generate single slice at 10 cm, output data.frame
s <- dice(d, 10 ~ name + p1 + p2 + p3, SPC = FALSE)

# generate integer slices from 0 - 26 cm
# note that slices are specified by default as "top-down"
# result is a SoilProfileCollection
# e.g. the lower depth will always by top + 1
s <- dice(d, fm = 0:25 ~ name + p1 + p2 + p3)
par(mar=c(0,1,0,1))
plotSPC(s)


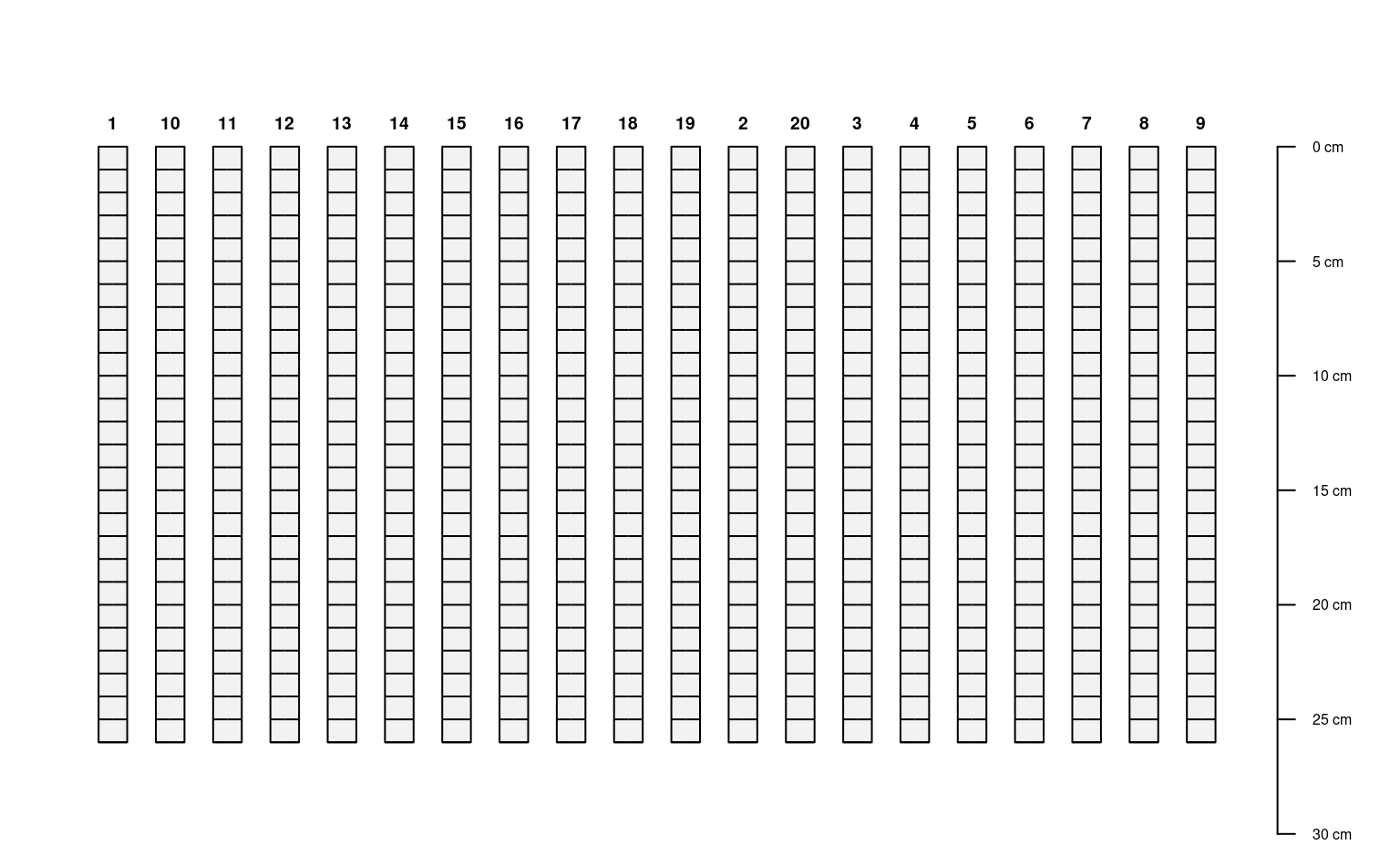# generate slices from 0 - 11 cm, for all variables
s <- dice(d, fm = 0:10 ~ .)
print(s)
#> SoilProfileCollection with 20 profiles and 220 horizons
#> profile ID: id  |  horizon ID: sliceID 
#> Depth range: 11 - 11 cm
#> 
#> ----- Horizons (6 / 220 rows  |  10 / 13 columns) -----
#>  id sliceID top bottom hzID name      p1        p2       p3        p4
#>   1       1   0      1    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#>   1       2   1      2    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#>   1       3   2      3    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#>   1       4   3      4    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#>   1       5   4      5    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#>   1       6   5      6    1   H1 -8.1148 -4.038598 2.344391 -4.589098
#> [... more horizons ...]
#> 
#> ----- Sites (6 / 20 rows  |  1 / 1 columns) -----
#>  id
#>   1
#>  10
#>  11
#>  12
#>  13
#>  14
#> [... more sites ...]
#> 
#> Spatial Data:
#> [EMPTY]

# compute percent missing, for each slice,
# if all vars are missing, then NA is returned
d$p1[1:10] <- NA
s <- dice(d, 10 ~ ., SPC = FALSE, pctMissing = TRUE)
head(s)
#>   hzID id top bottom name        p1          p2        p3         p4
#> 1    1  1  10     11   H1        NA  -4.0385981  2.344391  -4.589098
#> 2    5 10  10     11   H2        NA  -0.4422915 -3.941346  14.046647
#> 3    9 11  10     11   H2        NA -10.3652288 12.298109  -6.787727
#> 4   13 12  10     11   H1 12.247845   4.3251815  1.382016 -13.858707
#> 5   19 13  10     11   H1  4.109318   5.8979316 -3.498424  -4.977782
#> 6   24 14  10     11   H1  5.355912  -6.6952467  7.802510  -3.715831
#>            p5 sliceID .oldTop .oldBottom .pctMissing
#> 1   4.0915670      11       0         28   0.1666667
#> 2 -14.4513307      70       9         29   0.1666667
#> 3  -1.0061679     140       9         36   0.1666667
#> 4  -4.2897974     217       0         22   0.0000000
#> 5   0.4193661     342       0         28   0.0000000
#> 6   3.6439653     469       0         29   0.0000000

if (FALSE) {
##
## check sliced data
##

# test that mean of 1 cm slices property is equal to the
# hz-thickness weighted mean value of that property
data(sp1)
depths(sp1) <- id ~ top + bottom

# get the first profile
sp1.sub <- sp1[which(profile_id(sp1) == 'P009'), ]

# compute hz-thickness wt. mean
hz.wt.mean <- with(
  horizons(sp1.sub),
  sum((bottom - top) * prop) / sum(bottom - top)
)

# hopefully the same value, calculated via slice()
s <- dice(sp1.sub, fm = 0:max(sp1.sub) ~ prop)
hz.slice.mean <- mean(s$prop, na.rm = TRUE)

# they are the same
all.equal(hz.slice.mean, hz.wt.mean)
}